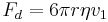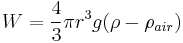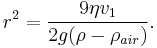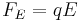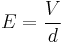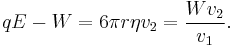Oil drop experiment

The oil drop experiment was an experiment performed by Robert Millikan and Harvey Fletcher in 1909 to measure the elementary electric charge (the charge of the electron).
The experiment entailed balancing the downward gravitational force with the upward buoyant and electric forces on tiny charged droplets of oil suspended between two metal electrodes. Since the density of the oil was known, the droplets' masses, and therefore their gravitational and buoyant forces, could be determined from their observed radii. Using a known electric field, Millikan and Fletcher could determine the charge on oil droplets in mechanical equilibrium. By repeating the experiment for many droplets, they confirmed that the charges were all multiples of some fundamental value, and calculated it to be 1.5924(17)×10−19 C, within one percent of the currently accepted value of 1.602176487(40)×10−19 C. They proposed that this was the charge of a single electron.
Contents |
Background

Starting in 1900, while a professor at the University of Chicago, Millikan, with the significant input of Fletcher[1], and after improving his setup, published his seminal study in 1913.[2]
His experiment measured the force on tiny charged droplets of oil suspended against gravity between two metal electrodes. Knowing the electric field, the charge on the droplet was determined. Repeating the experiment for many droplets, Millikan showed that the results could be explained as integer multiples of a common value (1.592×10−19 C), the charge on a single electron.
At the time of Millikan and Fletcher's oil drop experiments, the existence of subatomic particles was not universally accepted. Experimenting with cathode rays in 1897, J. J. Thomson had discovered negatively charged "corpuscles", as he called them, with a mass about 1000 times smaller than that of a hydrogen atom. Similar results had been found by George FitzGerald and Walter Kaufmann. Most of what was then known about electricity and magnetism, however, could be explained on the basis that charge is a continuous variable; in much the same way that many of the properties of light can be explained by treating it as a continuous wave rather than as a stream of photons.
The so-called elementary charge e is one of the fundamental physical constants and its accurate value is of great importance. In 1923, Millikan won the Nobel Prize in physics in part because of this experiment.
Aside from the measurement, the beauty of the oil drop experiment is that it is a simple, elegant hands-on demonstration that charge is actually quantized. Thomas Edison, who had previously thought of charge as a continuous variable, became convinced after working with Millikan and Fletcher's apparatus. This experiment has since been repeated by generations of physics students, although it is rather expensive and difficult to do properly.
Experimental procedure
Apparatus
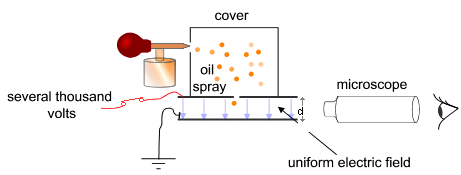
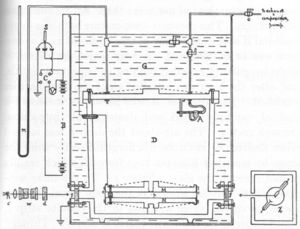
Robert Millikan’s apparatus incorporated a parallel pair of horizontal metal plates. By applying a potential difference across the plates, a uniform electric field was created in the space between them. A ring of insulating material was used to hold the plates apart. Four holes were cut into the ring, three for illumination by a bright light, and another to allow viewing through a microscope.
A fine mist of oil droplets was sprayed into a chamber above the plates. The oil was of a type usually used in vacuum apparatus and was chosen because it had an extremely low vapour pressure. Ordinary oil would evaporate away under the heat of the light source causing the mass of the oil drop to change over the course of the experiment. Some oil drops became electrically charged through friction with the nozzle as they were sprayed. Alternatively, charging could be brought about by including an ionising radiation source (such as an X-ray tube). The droplets entered the space between the plates and, because they were charged, could be made to rise and fall by changing the voltage across the plates.
Method
Initially the oil drops are allowed to fall between the plates with the electric field turned off. They very quickly reach a terminal velocity because of friction with the air in the chamber. The field is then turned on and, if it is large enough, some of the drops (the charged ones) will start to rise. (This is because the upwards electric force FE is greater for them than the downwards gravitational force W, in the same way bits of paper can be picked up by a charged rubber rod). A likely looking drop is selected and kept in the middle of the field of view by alternately switching off the voltage until all the other drops have fallen. The experiment is then continued with this one drop.
The drop is allowed to fall and its terminal velocity v1 in the absence of an electric field is calculated. The drag force acting on the drop can then be worked out using Stokes' law:
where v1 is the terminal velocity (i.e. velocity in the absence of an electric field) of the falling drop, η is the viscosity of the air, and r is the radius of the drop.
The weight W is the volume V multiplied by the density ρ and the acceleration due to gravity g. However, what is needed is the apparent weight. The apparent weight in air is the true weight minus the upthrust (which equals the weight of air displaced by the oil drop). For a perfectly spherical droplet the apparent weight can be written as:
Now at terminal velocity the oil drop is not accelerating. So the total force acting on it must be zero. So the two forces F and W must cancel one another out (that is, F = W). This implies
Once r is calculated, W can easily be worked out.
Now the field is turned back on, and the electric force on the drop is
where q is the charge on the oil drop and E is the electric field between the plates. For parallel plates
where V is the potential difference and d is the distance between the plates.
One conceivable way to work out q would be to adjust V until the oil drop remained steady. Then we could equate FE with W. But in practice this is extremely difficult to do precisely. Also, determining FE proves difficult because the mass of the oil drop is difficult to determine without reverting back to the use of Stokes' Law. A more practical approach is to turn V up slightly so that the oil drop rises with a new terminal velocity v2. Then
Fraud allegations
There is some controversy over the use of selectivity in Millikan's results of his second experiment measuring the electron charge raised by the historian Gerald Holton. Holton (1978) pointed out that Millikan disregarded a large set of the oil drops gained in his experiments without apparent reason. Allan Franklin, a former high energy experimentalist and current philosopher of science at the University of Colorado has tried to rebut this point by Holton[3]. Franklin contends that Millikan's exclusions of data did not affect the final value of e that Millikan obtained but concedes that there was substantial "cosmetic surgery" that Millikan performed which had the effect of reducing the statistical error on e. This enabled Millikan to quote the figure that he had calculated e to better than one half of one percent; in fact, if Millikan had included all of the data he threw out, it would have been to within 2%. While this would still have resulted in Millikan having measured e better than anyone else at the time, the slightly larger uncertainty might have allowed more disagreement with his results within the physics community. David Goodstein counters that Millikan plainly states that he only included drops which had undergone a "complete series of observations" and excluded no drops from this group.[4]
Millikan's experiment and cargo cult science
In a commencement address given at the California Institute of Technology (Caltech) in 1974 (and reprinted in Surely You're Joking, Mr. Feynman!), physicist Richard Feynman noted:
We have learned a lot from experience about how to handle some of the ways we fool ourselves. One example: Millikan measured the charge on an electron by an experiment with falling oil drops, and got an answer which we now know not to be quite right. It's a little bit off because he had the incorrect value for the viscosity of air. It's interesting to look at the history of measurements of the charge of an electron, after Millikan. If you plot them as a function of time, you find that one is a little bit bigger than Millikan's, and the next one's a little bit bigger than that, and the next one's a little bit bigger than that, until finally they settle down to a number which is higher.
Why didn't they discover the new number was higher right away? It's a thing that scientists are ashamed of - this history - because it's apparent that people did things like this: When they got a number that was too high above Millikan's, they thought something must be wrong - and they would look for and find a reason why something might be wrong. When they got a number close to Millikan's value they didn't look so hard. And so they eliminated the numbers that were too far off, and did other things like that. We've learned those tricks nowadays, and now we don't have that kind of a disease.[5][6]
As of 2008[update], the accepted value for the elementary charge is 1.602176487(40)×10−19 C,[7] where the 40 indicates the uncertainty of the last two decimal places. In his Nobel lecture, Millikan gave his measurement as 4.774(5)×10−10 statC,[8] which equals 1.5924(17)×10−19 C. The difference is less than one percent, but it is more than five times greater than Millikan's standard error, so the disagreement is significant.
References
- ↑ Elektrizitätsmengen, Phys. Zeit., 10(1910), p. 308
- ↑ Millikan, R. A. (1913). "On the Elementary Electric charge and the Avogadro Constant". Phys. Rev. 2 (2): 109–143. doi:10.1103/PhysRev.2.109.
- ↑ Franklin, A. (1997). "Millikan's Oil-Drop Experiments". The Chemical Educator 2 (1): 1–14. doi:10.1007/s00897970102a.
- ↑ Goodstein, D. (2000). "In defense of Robert Andrews Millikan". Engineering and Science (Pasadena, California: Caltech Office of Public Relations) 63 (4): 30–38. http://eands.caltech.edu/articles/Millikan%20Feature.pdf. Retrieved December 2009.
- ↑ Feynman, Richard, "Cargo Cult Science" (adapted from 1974 California Institute of Technology commencement address), Donald Simanek's Pages, Lock Haven University, rev. August 2008.
- ↑ Feynman, Richard Phillips; Leighton, Ralph; Hutchings, Edward (1997-04-01). "Surely you're joking, Mr. Feynman!": adventures of a curious character. New York: W. W. Norton & Company. p. 342. ISBN 9780393316049. http://books.google.com/books?id=7papZR4oVssC&pg=PA342. Retrieved 10 July 2010.
- ↑ NIST Reference on Constants, Units and Uncertainty
- ↑ Millikan, Robert A.. "The electron and the light-quant from the experimental point of view" Stockholm (May 23, 1924). Retrieved on 2006-11-12.
Further reading
- Serway, Raymond A.; Faughn, Jerry S. (2006). Holt: Physics. Holt, Rinehart and Winston. ISBN 0-03-073548-3.
- Thornton, Stephen T.; Rex, Andrew (2006). Modern Physics for Scientists and Engineers (3rd ed.). Brooks/Cole. ISBN 0-495-12514-8.
- Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th ed.). Brooks/Cole. ISBN 0-534-40842-7.
External links
- Thomsen, Marshall, "Good to the Last Drop". Millikan Stories as "Canned" Pedagogy. Eastern Michigan University.
- CSR/TSGC Team, "Quark search experiment". The University of Texas at Austin.
- The oil drop experiment appears in a list of Science's 10 Most Beautiful Experiments originally published in the New York Times.
- Engeness, T.E., "The Millikan Oil Drop Experiment". 25 April 2005
- Millikan R. A. (1913). "On the elementary electrical charge and the Avogadro constant". The Physical Review, Series II 2: 109–143. http://www.aip.org/history/gap/PDF/millikan.pdf., Paper by Millikan discussing modifications to his original experiment to improve its accuracy.
- Millikan Oil Drop Experiment in space. A variation of this experiment has been suggested for the International Space Station.